Guía de reglas topológicas implementadas en gvSIG
Introducción
A continuación se presenta una referencia de las reglas topológicas incluídas en la primera versión de la extensión de Topología y análisis vectorial avanzado de gvSIG. La parte de proceso topológico de este proyecto es realizada por la librería org.gvsig.topology.jar, generada por el proyecto libTopology, que define un marco de desarrollo extensible que permite a cualquier desarrollador introducir nuevas reglas topológicas (y / o alfanuméricas).
Seguidamente procedemos a describir cada una de las reglas introducidas en la primera versión de la extensíon.
Reglas topológicas implementadas en gvSIG
GEOMETRÍA JTS VÁLIDA.
-Descripción
Actualmente gvSIG trabaja para la mayor parte de sus operaciones con un modelo de geometrías que establece muy pocas restricciones topológicas, casi en "espaguetti". La principal ventaja de este modelo es que su nivel de abstracción es muy cercano al del API empleado para renderizar mapas (Java2D), lo que permite que gvSIG tenga una velocidad de renderizado de geometrías vectoriales muy elevada.
Un beneficio adicional de emplear un modelo de geometrías con pocas restricciones topológicas es que permite dibujar prácticamente la totalidad de orígenes de datos. Al establecer pocas restricciones topológicas, casi la totalidad de los datos cumplen estas restricciones y por tanto pueden ser dibujados sin problemas.
A la hora de realizar operaciones de geoprocesamiento vectorial gvSIG se apoya en la funcionalidad de la librería JTS [1], al igual que la gran mayoría del resto de proyectos SIG del stack OSGeo como UDIG, PostGIS, OpenJUMP, etc. JTS es una librería Java que trata de implementar (en un 99%) la especificación SFS de OGC, especificación que define un modelo de geometrías propio [2], mucho más restrictivo topológicamente que el modelo de geometrías de gvSIG.
El hecho de que el modelo de geometrías empleado por gvSIG para renderizar apenas introduzca restricciones topológicas hace que a la hora de aplicar funciones de análisis y geoprocesamiento sobre geometrías que sí podemos visualizar, en ocasiones nos encontremos con el efecto no deseado de que no podemos realizar estas operaciones, al no cumplir estas geometrías las restricciones topológicas impuestas por el modelo de JTS.
Esta regla topológica verifica que las geometrías de una capa vectorial verifican las restricciones topológicas impuestas por el modelo topológico de JTS, y que por tanto originarán geometrías JTS válidas.
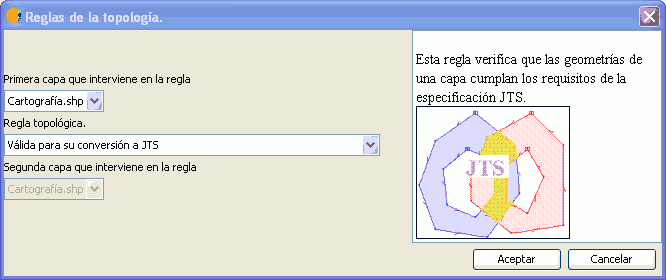
Regla: Valida para su conversión a JTS
-Número de capas que intervienen en la regla.
Una.
-Tipo de geometría de las capa
Indiferente.
-Correcciones predefinidas de los errores/incumplimientos
Eliminar: Borrar el Feature cuya geometría no cumple la regla.
LAS LÍNEAS NO PUEDE TENER NODOS COLGANTES.
-Descripción
Esta regla verifica que todas las geometrías de una capa de líneas conectan en sus extremos con otras geometrías de la misma capa. Los extremos de línea que no conecten con otras líneas generarán errores, conocidos en este caso como nodos colgantes.
Esta regla es de utilidad cuando las geometrías lineales de una capa deben formar circuitos cerrados, como por ejemplo los bordes de polígonos. De este modo, si queremos convertir una capa de líneas en una capa de polígonos que cubra completamente el espacio (sin huecos), podemos verificar si vamos a encontrar problemas en la conversión mediante esta regla. También es de utilidad en el caso de líneas que deben conectar con otras líneas, como los tramos de un callejero. En este caso, cuando un nodo colgante se corresponda con un fin de calle o callejón sin salida, los errores topológicos encontrados podrán ser marcados como excepciones.
Regla: Las líneas no pueden tener nodos colgantes
-Número de capas que intervienen en la regla.
Una.
-Tipo de geometría de las capa
Lineal.
-Correcciones predefinidas de los errores/incumplimientos
Extender nodo colgante hasta el nodo más próximo. Desplaza el nodo colgante hasta el nodo más próximo, siempre que la distancia de desplazamiento no supere un umbral determinado. Si se produce la corrección, garantiza que no se introducen pseudonodos.
Extender nodo colgante hasta el vértice más próximo. Igual que el anterior, pero el desplazamiento es hasta el vértice más próximo de otra geometría. Si se produce la corrección, se está introduciendo un pseudonodo (dos líneas que intersectan en un punto que no es nodo o extremo de línea).
LAS LÍNEAS NO PUEDEN TENER PSEUDONODOS.
-Descripción
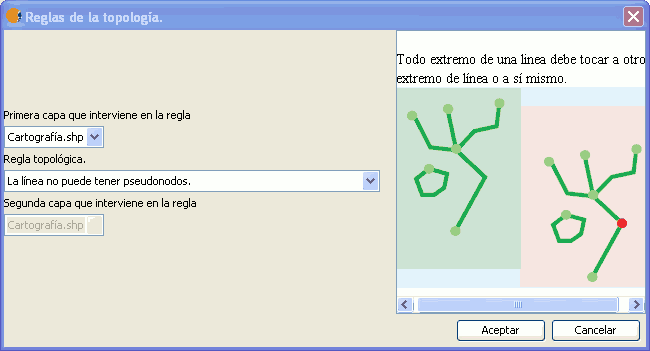
Verifica que todo extremo de una línea conecte al menos con dos líneas. Si una línea tiene un extremo (nodo) que solamente conecta con el extremo de otra línea, a este extremo se le conoce como pseudonodo. Este tipo de restricción topológica es util para modelar tramos de vias urbanas, en los que el fin de un trama aparece delimitado por la aparición de una bifurcación. La finalización del tramo en un punto en el que no existen bifurcaciones definiría un pseudonodo (que podría ser tolerado si se marca como excepción).
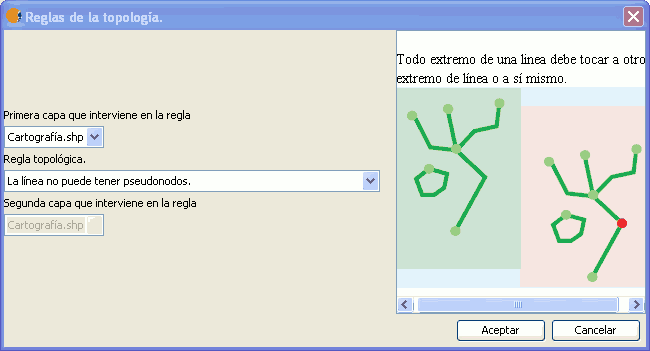
Regla: Las líneas no pueden tener pseudonodos.
Normalmente, en la literatura SIG también se ha conocido con el nombre de pseudonodo los casos en los que dos líneas intersectan en un punto que no es nodo de ambas líneas. Este tipo de pseudonodos no son detectados por esta regla topológica. El geoproceso "Limpiar topología" permite detectar este otro tipo de pseudonodos, y fragmentar las líneas originales para generar un conjunto de líneas conectadas en nodos.
Futuras versiones de la extensión de Topología de gvSIG incorporarán reglas topológicas para detectar este tipo de errores (Line must not intersect in non node points)
-Número de capas que intervienen en la regla.
Una.
-Tipo de geometría de las capa
Lineal.
-Correcciones predefinidas de los errores/incumplimientos
Eliminar pseudonodo. Fusiona las dos líneas que han originado el pseudonodo en una única línea.
LAS LÍNEAS NO PUEDEN TENER AUTOINTERSECCIONES.
-Descripción
Tanto el modelo de geometrías de renderizado de gvSIG (API de geometrias de FMap, muy próximo al API de geometrías de AWT/Java2D) como el modelo de geometrías de JTS permite que las geometrías lineales se autointersecten (aunque no las geometrías poligonales).
Esta regla permite añadir un grado de restricción adicional, verificando que las geometrías de una capa de líneas no puedan autointersectarse, a no ser que se trate de geometrías cerradas, no siendo por tanto la "autointersección" otra cosa que la coincidencia de los nodos de inicio y fin de la línea. Una autointersección es un tipo particular de pseudonodo de intersección (intersección de una línea consigo misma en un punto que no es nodo).
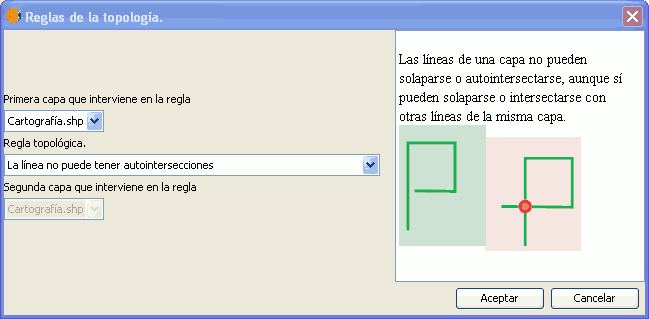
Regla: Las líneas no pueden tener autointersecciones
-Número de capas que intervienen en la regla.
Una.
-Tipo de geometría de las capa
Lineal.
-Correcciones predefinidas de los errores/incumplimientos
Fragmentar línea. Divide la línea que se autointersecta en el punto de autointersección, que pasará a ser nodo extremo de las nuevas líneas generadas.
LOS POLÍGONOS NO PUEDEN TENER AUTOINTERSECCIONES.
-Descripción
Esta restricción verifica que ninguno de los anillos (borde exterior o huecos) o partes de una geometría polígonal presenta autointersecciones.
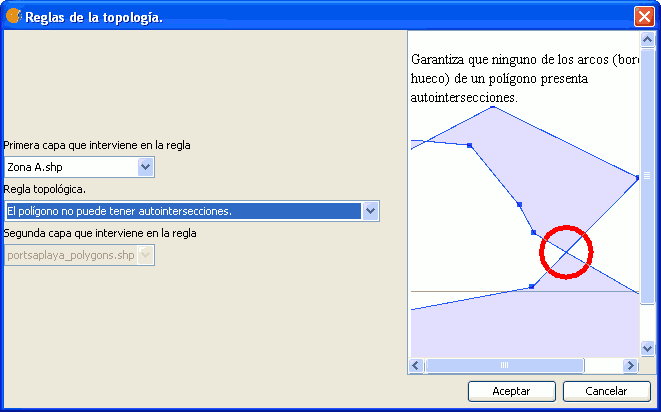
Regla: Los polígonos no pueden tener autointersecciones
-Número de capas que intervienen en la regla.
Una.
-Tipo de geometría de las capa
Poligonal.
-Correcciones predefinidas de los errores/incumplimientos
Fragmentar polígono por autointersecciones. Divide el polígono o superficie 2D que infringe la regla por sus puntos de autointersección. Siendo n el número de autointersecciones detectadas, se generarán n+1 polígonos.
LAS GEOMETRÍAS DE LA CAPA DE ORIGEN DEBEN ESTAR CONTENIDAS EN UNA GEOMETRÍA DE LA CAPA DESTINO.
-Descripción
Toda geometría de la capa A (origen) debe estar contenida en una geometría de la capa B (destino). Un caso típico de aplicación de esta regla lo encontramos para modelar divisiones administrativas (naciones) y subdivisiones de éstas (provincias). Un matiz que diferencia esta regla de la regla "las geometrías de A deben estar cubiertas por una geometría de B" es la la diferencia entre "contenido" y "cubierto". En la relación "contenido" el borde de la geometría contenida debe ser disjunto con el borde de la geometría contenedora.
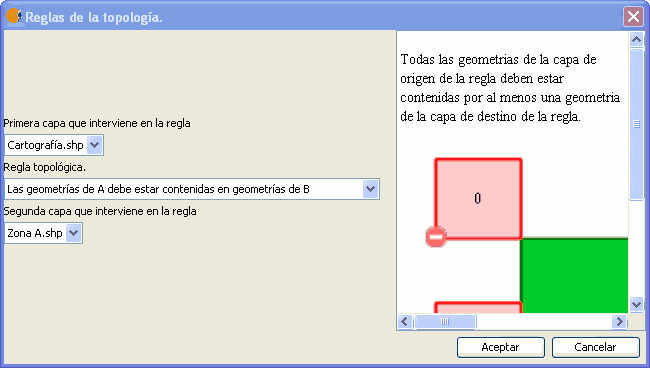
Regla: Las geometrías de A deben estar contenidas en geomtrias de B
-Número de capas que intervienen en la regla.
Dos.
-Tipo de geometría de las capa
Indiferente.
-Correcciones predefinidas de los errores/incumplimientos
Borrar elemento causante. Borra todas las geometrías de la capa A que no cumplen la regla.
LAS GEOMETRÍAS DE LA CAPA DE ORIGEN DEBEN ESTAR CUBIERTAS POR UNA GEOMETRÍA DE LA CAPA DESTINO.
-Descripción
Similar a la regla "Las geometrías de A deben estar contenidas en una geometría de B", con un matiz diferenciador: si una geometría de A recae en el borde de una geometría de B, estará cumpliendo la regla. Por ejemplo, si A es una capa de líneas, y B una capa de polígonos, y una geometría de A coincide con el borde de un polígono de B (o está cubierta por dicho borde), aunque dicha geometría de A no esté en el interior del polígono de B, estará cumpliendo la restricción topológica.
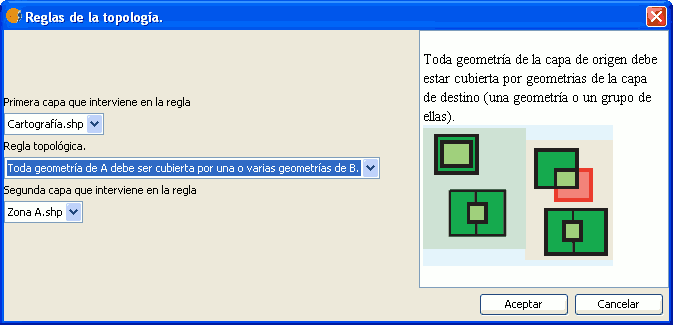
Regla: Toda geometría de A debe ser cubierta por una o varias geometrias de B
-Número de capas que intervienen en la regla.
Dos.
-Tipo de geometría de las capa
Indiferente.
-Correcciones predefinidas de los errores/incumplimientos
Borrar elemento causante. Borra todas las geometrías de la capa A que no cumplen la regla.
LAS GEOMETRÍAS DE LA CAPA DE ORIGEN DEBEN ESTAR CUBIERTAS POR LAS GEOMETRÍAS DE LA CAPA DE DESTINO.
-Descripción
Similar a la regla "Las geometrías de A deben estar cubiertas por una geometría de B", con la diferencia de que en este caso una geometría de A no tiene que estar cubierta por una única geometría de B, sino que cumplirá la restricción si es cubierta por varias geometrías.
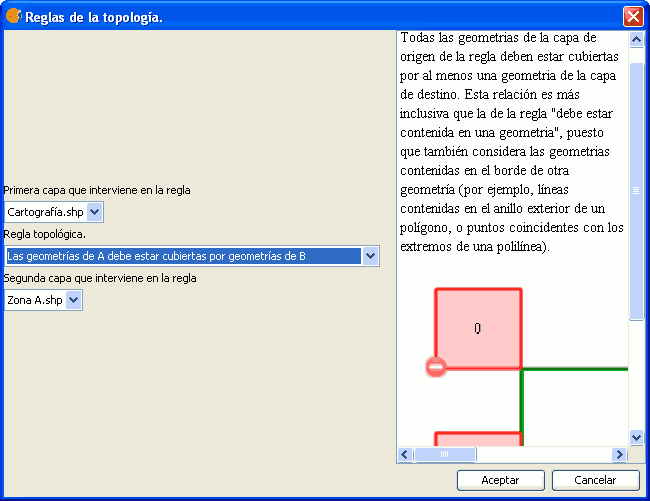
Regla: Las geometrias de A deben estar cubiertas por las geometrías de B
-Número de capas que intervienen en la regla.
Dos.
-Tipo de geometría de las capa
Indiferente.
-Correcciones predefinidas de los errores/incumplimientos
Borrar elemento causante. Borra todas las geometrías de la capa A que no cumplen la regla.
LAS GEOMETRÍAS DE LA CAPA DE ORIGEN DEBE TENER UNA GEOMETRÍA EQUIVALENTE (IGUAL) EN LA CAPA DE DESTINO.
-Descripción
Esta regla topológica sirve para detectar cambios o modificaciones entre diferentes versiones de una misma capa. Fuerza a que toda geometría de una capa tenga una geometría equivalente en otra capa. Si no se cumple esta restricción, se han introducido modificaciones.
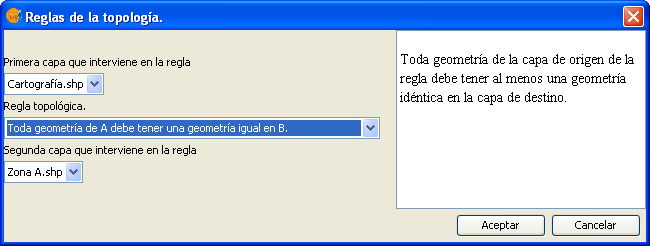
Regla: Toda geometría de A debe tener una geometria igual en B
-Número de capas que intervienen en la regla.
Dos.
-Tipo de geometría de las capa
Indiferente.
-Correcciones predefinidas de los errores/incumplimientos
Borrar elemento causante. Borra todas las geometrías de la capa A que no cumplen la regla.
LAS GEOMETRÍAS DE LA CAPA DE ORIGEN DEBEN CONTENER AL MENOS UNA GEOMETRÍA DE LA CAPA DE DESTINO.
-Descripción
Toda geometría de A debe contener al menos una geometría de B. Esta regla puede ser de utilidad para garantizar la integridad "entre capas" cuando una capa es el resultado de aplicar un geoproceso a otra capa. Por ejemplo, si calculamos el buffer de una capa de puntos, los polígonos de la capa resultante deben contener al menos un punto de la capa de partida.
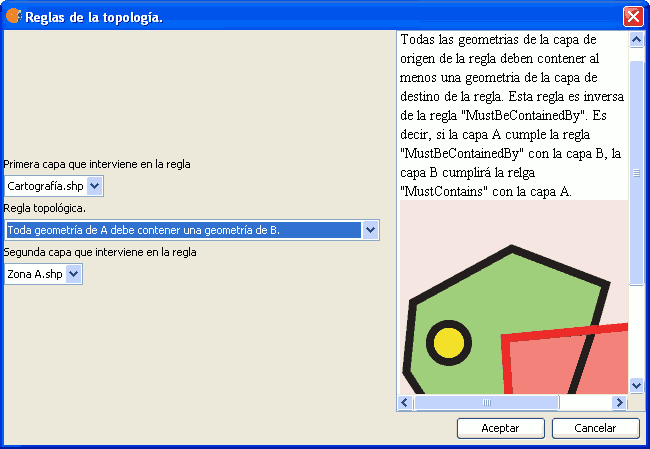
Regla: Toda geometría de A debe contener una geometría de B
-Número de capas que intervienen en la regla.
Dos.
-Tipo de geometría de las capa
Indiferente.
-Correcciones predefinidas de los errores/incumplimientos
Borrar elemento causante. Borra todas las geometrías de la capa A que no cumplen la regla.
LAS GEOMETRÍAS DE LA CAPA DE ORIGEN DEBEN CUBRIR AL MENOS UNA GEOMETRÍA DE LA CAPA DE DESTINO.
-Descripción
Equivalente a la regla anterior "las geometrías de A deben contener al menos una geometría de B". El matiz está en la diferencia entre "contener" y "cubrir". Supongamos que tenemos una capa con las principales ciudades unidas por ferrocarril, de puntos, y una capa de líneas con las líneas de ferrocarril de primer orden que unen estas ciudades. Esta regla nos permitiría garantizar que no hay líneas de ferrocarril de primer orden que no cubran ciudades.
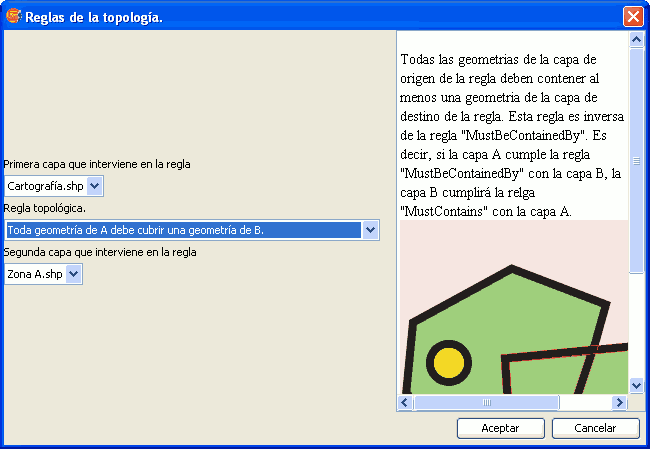
Regla: Toda geometría de A debe cubrir al menos una geometría de B.
-Número de capas que intervienen en la regla.
Dos.
-Tipo de geometría de las capa
Indiferente.
-Correcciones predefinidas de los errores/incumplimientos
Borrar elemento causante. Borra todas las geometrías de la capa A que no cumplen la regla.
LAS GEOMETRÍAS DE LA CAPA DE ORIGEN DEBEN CRUZARSE AL MENOS CON UNA GEOMETRÍA DE LA CAPA DE DESTINO.
-Descripción
Esta regla trata de garantizar que toda geometría de la capa A se cruce con al menos una geometría de la capa B. Una geometría se cruza con otra si comparte algunos puntos de su interior, aunque no todos.
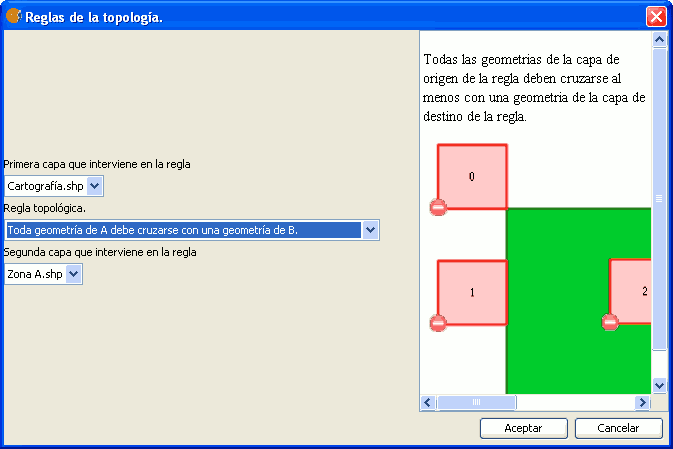
Regla: Toda geometría de A debe cruzarse al menos con una geometría de B
-Número de capas que intervienen en la regla.
Dos.
-Tipo de geometría de las capa
Indiferente.
Solo hay que tener en cuenta un matiz: si aplicamos esta regla para dos capas de puntos, solamente se cruzarán aquellas geometrías que sean coincidentes.
-Correcciones predefinidas de los errores/incumplimientos
Borrar elemento causante. Borra todas las geometrías de la capa A que no cumplen la regla.
LAS GEOMETRÍAS DE LA CAPA DE ORIGEN DEBEN SER DISJUNTAS CON LAS GEOMETRÍAS DE LA CAPA DE DESTINO.
-Descripción
Esta regla topológica sirve para verificar que las geometrías de la capa A no compartan ningún punto con las geometrías de la capa B. Si alguna geometría de A comparte al menos un punto con una geometría de B, ya no serán disjuntas y se estará incumpliendo la regla.
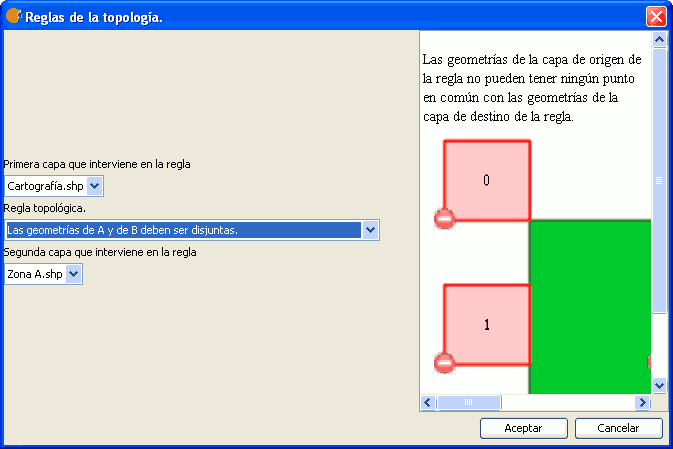
Regla: Las geometrias de A y B seben ser disjuntas.
-Número de capas que intervienen en la regla.
Dos.
-Tipo de geometría de las capa
Indiferente.
-Correcciones predefinidas de los errores/incumplimientos
Borrar elemento causante. Borra todas las geometrías de la capa A que no cumplen la regla.
LAS GEOMETRÍAS DE UNA CAPA NO PUEDEN TENER DUPLICADOS.
-Descripción
Esta regla topológica trata de garantizar que dentro de una misma capa no haya dos geometrías iguales, o cuya similaridad sea tan elevada que puedan llegar a ser consideradas iguales. En este sentido, los criterios de similaridad variarán según el tipo de la geometría de la capa:
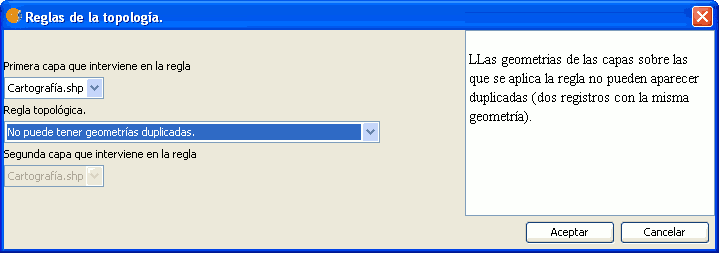
Regla: No puede tener geometrías duplicadas.
- Para capas de puntos: dos puntos son iguales si tiene las mismas coordenadas, o se encuentran separados por una distancia inferior a la distancia de cluster de la topología.
- Para capas de líneas: dos líneas son iguales si tienen el mismo número vértices, y las coordenadas de estos son iguales. En el caso de que esto no suceda, se aplica el criterio de la "banda epsilon". Cada una de las líneas a comparar define una banda, resultado de obtener un buffer de la línea empleando como distancia de buffer la tolerancia de cluster. Si la banda de una línea contiene completamente a la banda de la otra línea, se considerará que las líneas son equivalente. Finalmente, si ambas bandas se solapan en una proporción superior a un umbral porcentual, también se considerarán equivalentes (el umbral implementado actualmente es del 85%. En futuras versiones de la extensión de Topología se podrá especificar este umbral en la página de preferencias de la extensión).
- Para capas de polígonos: dos poligonos son iguales si sus bordes tienen el mismo número de vértices, sus coordenadas son iguales, e idéntico criterio se cumple para sus huecos. Si no se verifica la igualdad, la regla aplicará una ponderación de los criterios de similaridad de polígonos definidos por el proyecto JCS (Jcs Conflation Suite), accesibles en [3], siendo concretamente:
- Distancia entre centroides. Cuanto menor sea esta distancia, más similares serán los dos polígonos comparados.
- Distancia Hausdorff. Longitud de la mayor desviación local de las dos geometrías. Cuanto menor sea esta distancia, mayor será la similitud entre las dos geometrías.
- Diferencia simétrica. La diferencia simétrica de un polígono respecto del otro está constituido por las áreas de éste que no se solapan con el otro. Cuanto menor sea la diferencia simétrica entre dos polígonos, mayor será su similaridad.
- Compacidad. El índice de compacidad de cada polígono es el ratio área/perimetro. Cuanto menor sea la diferencia de compacidad entre los dos polígonos, mayor será su similaridad.
- Histograma angular. El histograma angular de un polígono es el histograma de los ángulos que los segmentos del polígono forman con el eje x cartesiano, ponderado con la longitud del segmento. Cuanto mayor sea la similaridad de los histogramas angulares de dos polígonos, mayor será la similaridad de estos.
-Número de capas que intervienen en la regla.
Una.
-Tipo de geometría de las capa
Indiferente.
-Correcciones predefinidas de los errores/incumplimientos
Borrar elemento causante. Borra todas las geometrías de la capa A que no cumplen la regla.
LAS GEOMETRÍAS DE LA CAPA DE ORIGEN DEBEN TOCAR AL MENOS UNA GEOMETRÍA DE LA CAPA DE DESTINO.
-Descripción
Este regla pretende garantizar la mínima condición para que dos capas no sean disjuntas: que las geometrías de A se toquen al menos con una de las geometrías de B. Dos geometrías se tocan si tienen al menos un punto en común pero sus interiores no intersectan. Si consideramos una capa con edificios, y otra con muros que rodean a éstos, esta regla nos permitirá garantizar que todo muro debe tocar un edificio.
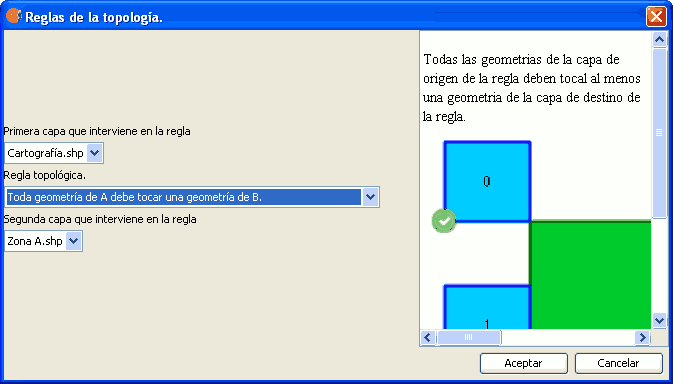
Regla: Toda geometrías de A debe tocar una geometría de B
-Número de capas que intervienen en la regla.
Dos.
-Tipo de geometría de las capa
Indiferente.
-Correcciones predefinidas de los errores/incumplimientos
Borrar elemento causante. Borra todas las geometrías de la capa A que no cumplen la regla.
LAS GEOMETRÍAS DEBEN SER MAYORES QUE LA TOLERANCIA CLUSTER.
-Descripción
Esta regla trata de garantizar que una capa no contiene geometrías espúreas o residuales. La consideración de que una geometría es residual, y no debe ser tenida en cuenta en una capa, se hace a partir de la tolerancia de cluster de la topología (que sería equivalente a las dimensiones de la minima unidad cartografiable), en función del tipo de geometría:
- Una geometría líneal será considerada espúrea si su longitud es inferior a la tolerancia de cluster. Todos los vértices que se encuentren a una distancia entre ellos inferior a la tolerancia de cluster serán colapsados.
- Una geometría polígonal será espúrea si su superficie es inferior al cuadrado de la tolerancia de cluster.
-Número de capas que intervienen en la regla.
Una.
-Tipo de geometría de las capa
Lineal (dimensión = 1) o poligonal (dimension = 2).
-Correcciones predefinidas de los errores/incumplimientos
Borrar elemento causante. Borra todas las geometrías de la capa A que no cumplen la regla.
LAS GEOMETRÍAS NO PUEDEN TENER PUNTOS CONSECUTIVOS REPETIDOS.
-Descripción
Tanto el modelo de geometrías de JTS como el modelo de geometrías definido por gvSIG en su librería vectorial FMap, permite que una geometría tenga coordenadas consecutivas repetidas. Esta regla trata de añadir un nivel adicional de restricción detectando aquellas ocurrencias de geometrías con coordenadas consecutivas repetidas, con el objetivo de corregirlas.
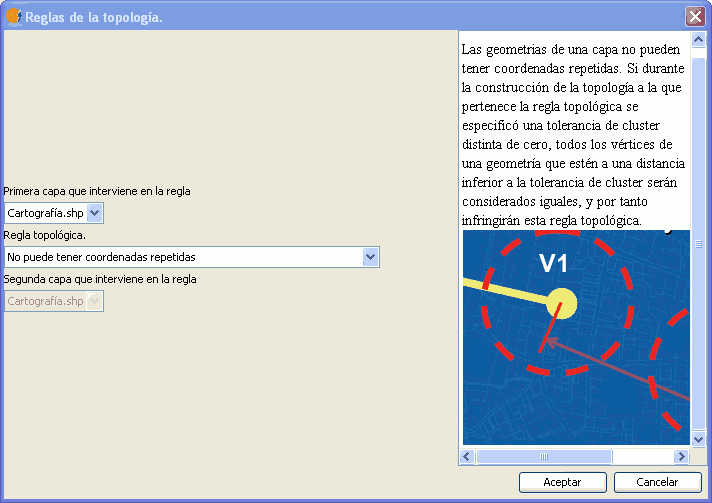
Regla: No puede tener coordenadas repetidas.
-Número de capas que intervienen en la regla.
Una.
-Tipo de geometría de las capa
Lineal o poligonal.
-Correcciones predefinidas de los errores/incumplimientos
Eliminar coordenadas repetidas. Genera una geometría equivalente a la original sin coordenadas consecutivas repetidas.
LOS PUNTOS NO PUEDEN SOLAPARSE.
-Descripción
Esta regla verifica que en una capa de puntos no existen puntos situados entre sí a una distancia inferior a la tolerancia de cluster.
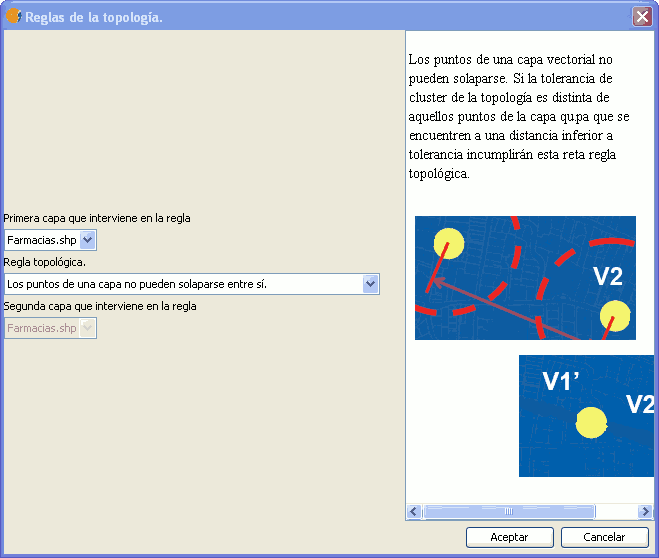
Regla: Los puentos de una misma capa no pueden solaparse entre si.
-Número de capas que intervienen en la regla.
Una.
-Tipo de geometría de las capa
Puntual (dimensión cero).
-Correcciones predefinidas de los errores/incumplimientos
Borrar elemento causante. Borra todas las geometrías de la capa A que no cumplen la regla.
LOS POLÍGONOS NO PUEDEN SOLAPARSE.
-Descripción
Esta regla trata de garantizar que los polígonos de una capa no se solapan entre sí, de tal forma que la intersección entre dos polígonos de una misma capa solo podrá ser un punto o una línea, nunca otro polígono. Esta regla, en combinación con la regla "los polígonos de una capa no pueden presentar huecos" asegura que una capa de polígonos cubre totalmente el espacio, sin solapamientos entre polígonos. Ambas reglas permiten emular el comportamiento del modelo topológico de coberturas (implementado en las versiones antiguas del software de ESRI) para capas de polígonos.
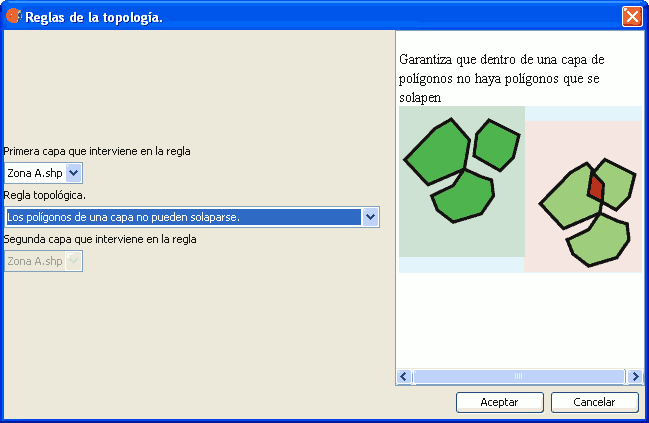
Regla: Los polígonos de una capa no pueden solaparse
-Número de capas que intervienen en la regla.
Una.
Tipo de geometría de las capa
Poligonal (2 Dimensiones).
-Correcciones predefinidas de los errores/incumplimientos
- Eliminar área de solape. Substrae el área de solape de los dos polígonos que originan el error.
- Crear nuevo polígono. Crea un nuevo feature de geometría poligonal con el área de solape, substrayendo esta área de los dos poligonos que originaron el error.
- Añadir solape a uno de los dos polígonos. Añade el área de solape a uno de los dos polígonos, substrayéndosela al otro polígono. Esta corrección no es completamente automatizada, y requiere de la intervención del usuario. Cuando se activa esta opción desde el menú desplegable, se muestra un diálogo. Accionando en este diálogo el botón "seleccionar geometría que perderá el área", se podrá seleccionar sobre el mapa la geometría que perderá el área de solape. Seguidamente, pulsando aceptar se producirá la corrección.
LOS POLÍGONOS DE LA CAPA DE ORIGEN NO PUEDEN SOLAPARSE CON LOS POLÍGONOS DE LA CAPA DE DESTINO.
-Descripción
Esta regla trata de garantizar que los polígonos de dos capas guardan cierta relación, de tal forma que no se solapen. Esto es de utilidad, por ejemplo, cuando tenemos divisiones administrativas de diferente nivel (naciones, provincias) y queremos que las de inferior jerarquía estén contenidas en las de superior jerarquía sin solaparse.
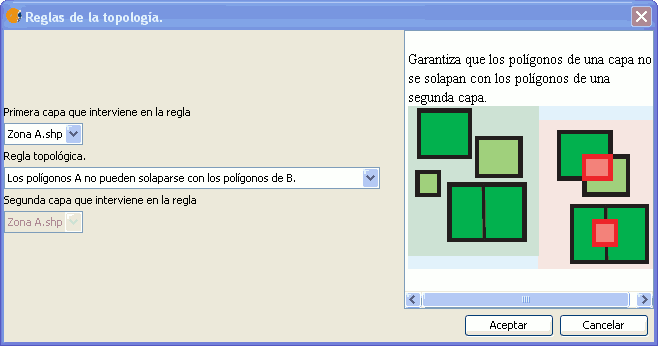
Regla: Los polígonos de A no pueden solaparse con los polígonos de B
-Número de capas que intervienen en la regla.
Dos.
-Tipo de geometría de las capa
Poligonal.
-Correcciones predefinidas de los errores/incumplimientos
- Añadir solape a uno de los dos polígonos. Añade el área de solape a uno de los dos polígonos, substrayéndosela al otro polígono. Esta corrección no es completamente automatizada, y requiere de la intervención del usuario. Cuando se activa esta opción desde el menú desplegable, se muestra un diálogo. Accionando en este diálogo el botón "seleccionar geometría que perderá el área", se podrá seleccionar sobre el mapa la geometría que perderá el área de solape. Seguidamente, pulsando aceptar se producirá la corrección.
- Eliminar área de solape. Substrae el área de solape de los dos polígonos que originan el error.
LAS GEOMETRÍAS (LÍNEAS O POLÍGONOS) DEBEN SER CERRADAS.
-Descripción
Esta regla trata de garantizar que una geometría es cerrada (su primer y último punto coinciden), considerando una tolerancia de cluster dada. Para el caso de capas de polígonos, garantiza la corrección de éstas, como paso previo a cualquier proceso de análisis. Para el caso de capas de líneas, la verificación de esta regla es un paso previo conveniente previo a la conversión a capa de polígonos.
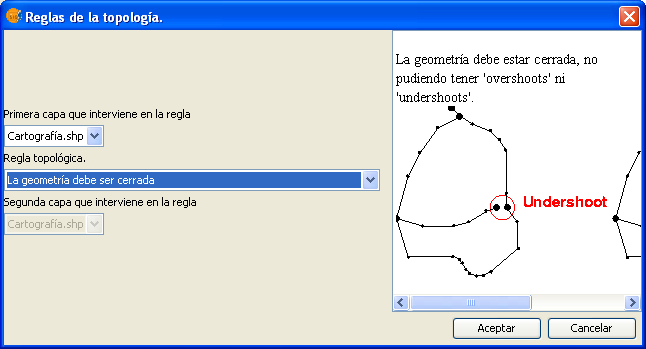
Regla: Las geometrías deben ser cerradas
-Número de capas que intervienen en la regla.
Una.
-Tipo de geometría de las capa
Lineal o poligonal.
-Correcciones predefinidas de los errores/incumplimientos
- Eliminar overshoot. Si la geometría cierra áreas, pero el último punto no coincide con el primero, se elimina el segmento sobrante.
- Añadir undershoot. Si la geometría no cierra áras, se añade un segmento que una el último punto con el primero.
LA CAPA DE POLÍGONOS NO PUEDE PRESENTAR HUECOS.
-Descripción
Esta regla permite garantizar que las geometrías poligonales de una capa cubren completamente el espacio, de tal forma que no existe ninguna zona no cubierta. Aquellas zonas no cubiertas constituirán huecos.
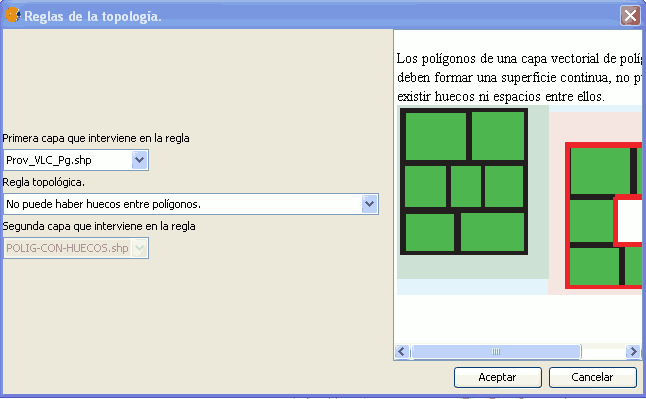
Regla: La capa de polígonos no puede tener huecos
Número de capas que intervienen en la regla.
Una.
-Tipo de geometría de las capa
Poligonal.
-Correcciones predefinidas de los errores/incumplimientos
Añadir nuevo polígono. Por cada hueco detectado, se creará un nuevo feature cuya geometría será el polígono del hueco.